

北京时间9月26日(周日)上午,将门-TechBeat人工智能社区很高兴邀请到美国西北大学助理教授——汪昭然老师和他的同学们,来到腾讯会议直播间,与大家分享他们组在本次ICML上以及其他的相关工作!
* 本次直播活动需要报名,报名通过审核后获得腾讯会议地址并加入活动交流群~
嘉宾介绍
汪昭然,美国西北大学工业工程、管理科学和计算机科学系(自2018年起)的助理教授,隶属于深度学习和优化统计学习中心。本科毕业于清华大学电子工程系,随后前往普林斯顿大学运筹与金融工程系攻读博士学位。
个人主页:https://zhaoranwang.github.io/
汪昭然所在的Northwestern Data-Driven Decision-Making Group,研究的长期目标是发展新一代数据驱动的决策方法、理论和系统,使人工智能适应紧迫的社会挑战。为此,研究目的是在关键领域,使深度强化学习在计算和统计上更有效;同时,规模化发展深度强化学习,设计和优化多智能体系统,特别是涉及人工和机器人之间协作或竞争的系统。基于这一目标,中心的研究兴趣涵盖机器学习、优化、统计学、博弈论和信息论。
欢迎博士生/博士后/实习生/访问学生申请以及产业合作。
更多详情:
https://en.wikipedia.org/wiki/Northwestern_University#/media/File:Northwestern_University_seal.svg
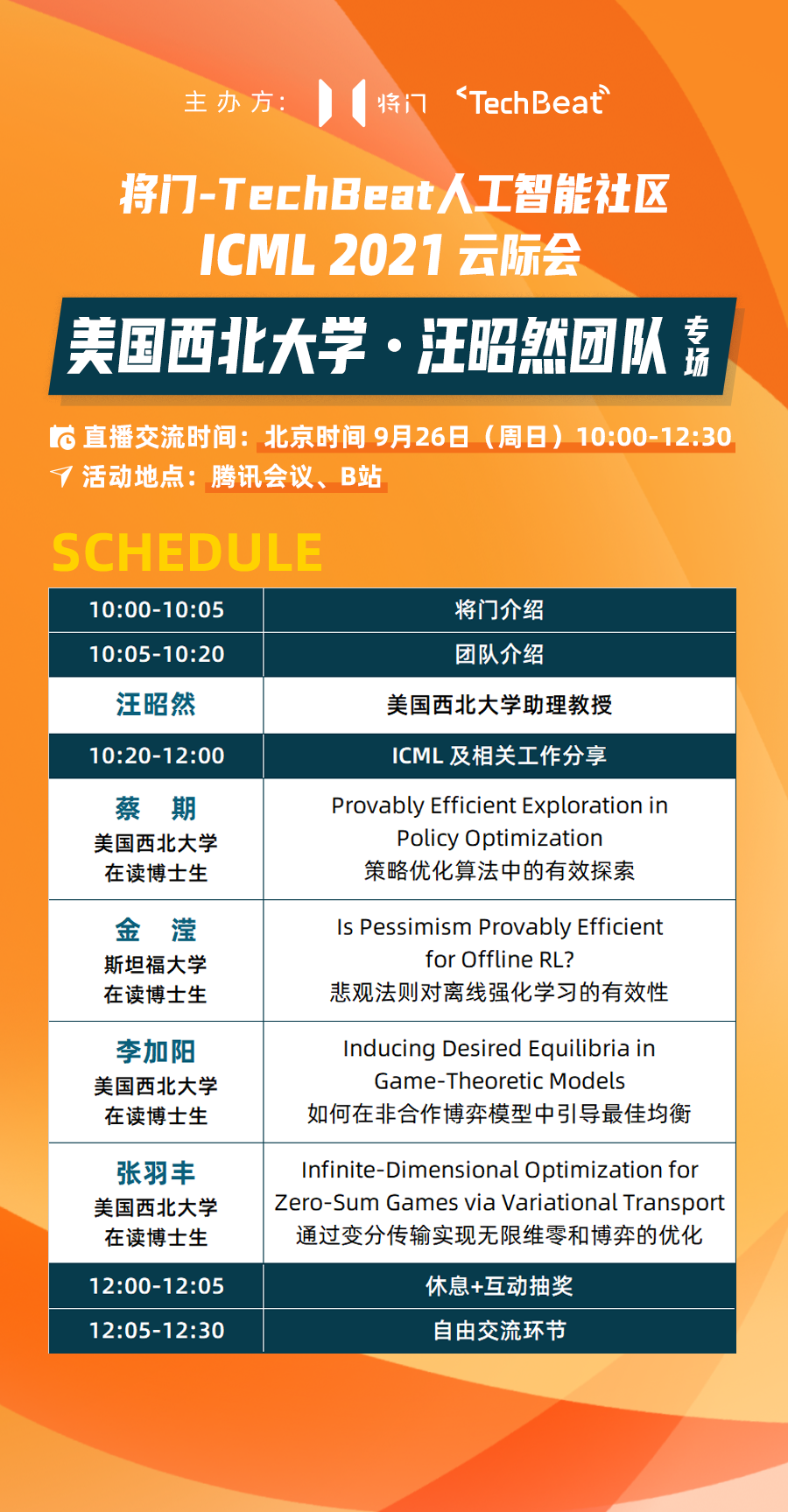
工作分享&嘉宾介绍
Provably Efficient Exploration
in Policy Optimization
策略优化算法中的有效探索
主讲人:蔡期-美国西北大学·在读博士生
虽然基于策略优化的强化学习算法在实践中取得了巨大的成功,但我们对它在理论上的有效性却了解甚少,尤其是相比于与另一类基于值方法的强化学习算法。本文提出了一种新的策略优化算法,它是策略梯度算法的一种“乐观”变体。我们在理论上证明了它在线性马尔可夫过程中可以充分高效地利用样本以学习最佳策略。
论文链接:
https://arxiv.org/abs/1912.05830
Is Pessimism Provably Efficient for Offline RL?
悲观法则对离线强化学习的有效性
主讲人:金滢-斯坦福大学·三年级博士生
这篇文章研究离线强化学习问题,即如何借助静态数据集来学习在未来环境下表现得好的行为准则,尤其是在对静态数据集完备性的较弱假设下学习足够好的准则。我们提出了基于悲观准则的值函数循环估计和学习方法,根据静态数据集为状态-行为值函数构建置信下界,并选取置信下界最高的作为行为准则。
论文链接:
https://arxiv.org/abs/2012.15085
Inducing Desired Equilibria
in Game-Theoretic Models
如何在非合作博弈模型中引导最佳均衡
主讲人:李加阳-美国西北大学·在读博士生
在社会系统中,自私的参与者可以被看作进行非合作博弈,并收敛到Nash均衡。然而,与社会最优结果相比,均衡有时是低效的。为了引导这些参与者达到理想的均衡(例如,使社会福利最大化的均衡),一个权威者(通常是代表公众的“政府”)可以引入纠正政策(通常以经济激励的形式出现)。在我们近期的论文中,我们研究了机器学习的最新进展如何帮助权威者更有效地引导预期中的均衡。
论文链接:
End-to-end Learning and Intervention in Games
https://proceedings.neurips.cc/paper/2020/file/c21f4ce780c5c9d774f79841b81fdc6d-Paper.pdf
Anticipate but Don't Solve: Provably Efficient Incentivization in Games by Designing-While-Playing
会在这周或下周上arXiv
Infinite-Dimensional Optimization for
Zero-Sum Games via Variational Transport
通过变分传输实现无限维零和博弈的优化
主讲人:张羽丰-美国西北大学·在读博士生
当决策变量位于有限维空间中时,博弈优化已被广泛研究,其解对应于纳什均衡 (NE) 下的纯策略,而梯度下降上升 (GDA) 方法在实践中广泛适用。在本文中,我们通过在连续变量集上定义的概率测度空间上的最小-最大分布优化问题来考虑无限维零和游戏,我们在功能空间中提出了一种基于 GDA 的基于粒子的变分传输算法。我们通过可证明有效的基于粒子的方法为解决无限维零和游戏提供了完整的统计和优化保证。
论文链接:
在线交流报名·注意事项
*请仔细阅读
1. 请保证所填信息的真实性和准确性,方便主办方进行审核;
2. 报名通过审核后将收到主办方的微信/邮件/通知,请保持手机和邮箱畅通;
3. 由于报名人数较多,主办方审核需要一定时间,请耐心等待~

北京时间9月26日(周日)上午,将门-TechBeat人工智能社区很高兴邀请到美国西北大学助理教授——汪昭然老师和他的同学们,来到腾讯会议直播间,与大家分享他们组在本次ICML上以及其他的相关工作!
* 本次直播活动需要报名,报名通过审核后获得腾讯会议地址并加入活动交流群~
嘉宾介绍
汪昭然,美国西北大学工业工程、管理科学和计算机科学系(自2018年起)的助理教授,隶属于深度学习和优化统计学习中心。本科毕业于清华大学电子工程系,随后前往普林斯顿大学运筹与金融工程系攻读博士学位。
个人主页:https://zhaoranwang.github.io/
汪昭然所在的Northwestern Data-Driven Decision-Making Group,研究的长期目标是发展新一代数据驱动的决策方法、理论和系统,使人工智能适应紧迫的社会挑战。为此,研究目的是在关键领域,使深度强化学习在计算和统计上更有效;同时,规模化发展深度强化学习,设计和优化多智能体系统,特别是涉及人工和机器人之间协作或竞争的系统。基于这一目标,中心的研究兴趣涵盖机器学习、优化、统计学、博弈论和信息论。
欢迎博士生/博士后/实习生/访问学生申请以及产业合作。
更多详情:
https://en.wikipedia.org/wiki/Northwestern_University#/media/File:Northwestern_University_seal.svg

工作分享&嘉宾介绍
Provably Efficient Exploration
in Policy Optimization
策略优化算法中的有效探索
主讲人:蔡期-美国西北大学·在读博士生
虽然基于策略优化的强化学习算法在实践中取得了巨大的成功,但我们对它在理论上的有效性却了解甚少,尤其是相比于与另一类基于值方法的强化学习算法。本文提出了一种新的策略优化算法,它是策略梯度算法的一种“乐观”变体。我们在理论上证明了它在线性马尔可夫过程中可以充分高效地利用样本以学习最佳策略。
论文链接:
https://arxiv.org/abs/1912.05830
Is Pessimism Provably Efficient for Offline RL?
悲观法则对离线强化学习的有效性
主讲人:金滢-斯坦福大学·三年级博士生
这篇文章研究离线强化学习问题,即如何借助静态数据集来学习在未来环境下表现得好的行为准则,尤其是在对静态数据集完备性的较弱假设下学习足够好的准则。我们提出了基于悲观准则的值函数循环估计和学习方法,根据静态数据集为状态-行为值函数构建置信下界,并选取置信下界最高的作为行为准则。
论文链接:
https://arxiv.org/abs/2012.15085
Inducing Desired Equilibria
in Game-Theoretic Models
如何在非合作博弈模型中引导最佳均衡
主讲人:李加阳-美国西北大学·在读博士生
在社会系统中,自私的参与者可以被看作进行非合作博弈,并收敛到Nash均衡。然而,与社会最优结果相比,均衡有时是低效的。为了引导这些参与者达到理想的均衡(例如,使社会福利最大化的均衡),一个权威者(通常是代表公众的“政府”)可以引入纠正政策(通常以经济激励的形式出现)。在我们近期的论文中,我们研究了机器学习的最新进展如何帮助权威者更有效地引导预期中的均衡。
论文链接:
End-to-end Learning and Intervention in Games
https://proceedings.neurips.cc/paper/2020/file/c21f4ce780c5c9d774f79841b81fdc6d-Paper.pdf
Anticipate but Don't Solve: Provably Efficient Incentivization in Games by Designing-While-Playing
会在这周或下周上arXiv
Infinite-Dimensional Optimization for
Zero-Sum Games via Variational Transport
通过变分传输实现无限维零和博弈的优化
主讲人:张羽丰-美国西北大学·在读博士生
当决策变量位于有限维空间中时,博弈优化已被广泛研究,其解对应于纳什均衡 (NE) 下的纯策略,而梯度下降上升 (GDA) 方法在实践中广泛适用。在本文中,我们通过在连续变量集上定义的概率测度空间上的最小-最大分布优化问题来考虑无限维零和游戏,我们在功能空间中提出了一种基于 GDA 的基于粒子的变分传输算法。我们通过可证明有效的基于粒子的方法为解决无限维零和游戏提供了完整的统计和优化保证。
论文链接:
在线交流报名·注意事项
*请仔细阅读
1. 请保证所填信息的真实性和准确性,方便主办方进行审核;
2. 报名通过审核后将收到主办方的微信/邮件/通知,请保持手机和邮箱畅通;
3. 由于报名人数较多,主办方审核需要一定时间,请耐心等待~

抱歉,您来晚了,活动结束了
|
订单总金额 ¥19999.00 请输入您的个人联系方式 |